Voila, j'ai comparé avec mes calculs.
J'avais calculé 21 couples étalon dont j'avais eu besoin, mais en fait, à partir des données Gaia DR2. Les écarts avec tes résultats vont jusqu'à 0,058'' en séparation et 0.074° en position.
J'ai retenu les 5 couples avec les écarts les plus importants et j'ai repris les calculs avec les mesures Gaia DR3. Les écarts diminuent souvent, mais pas toujours.
Voici le bilan avant prise en compte de la précession :
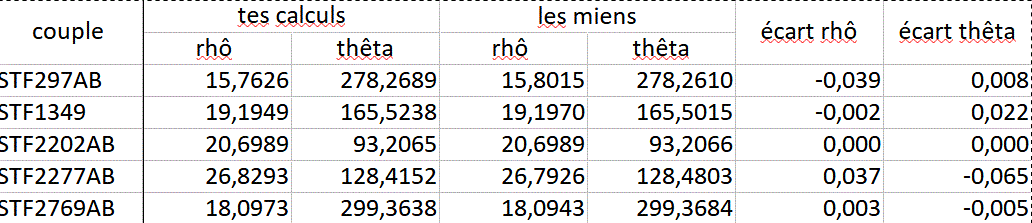
- tableau.gif (26.1 Kio) Consulté 139433 fois
STF297AB
Plusieurs mesures manquent dans la DR3 pour l'étoile primaire, dont les vitesses propres. J'ai pris les mesures de la DR2 à la place, elles sont proches de celles d'Hipparcos en ascension droite, pas trop en déclinaison, mais à mon avis c'est moins faux de prendre les mesures DR2 que de prendre zéro. Il faudra vérifier quand la DR4 sera sortie. Avec thêta proche de 270°, ceci devrait surtout impacter les résultat en position ... et nous trouvons des résultats proches (à 0,008° près).
En fait c'est en séparation qu'on a un désaccord de l'ordre de 0,04'', voir ci-après.
Ecarts en séparation
A mon avis, les écarts doivent provenir des formules de trigo : nous n'utilisons pas les mêmes. Jean Meeus dans les "
Calculs astronomiques à l’usage des amateurs" éditions 2014, recommande d'utiliser la formule approchée ρ2 = (Δα . cosδ)2 + (Δδ)2 dans le cas des petits angles proches de 0° ou de 180°. Il déconseille la formule en arc cos car dans ce cas |cosρ| est très proche de 1 et varie très lentement avec ρ ce qui entraîne un manque de précision dans les calculs numériques.
Ecarts en position
Je n'utilise pas non plus la même formule que toi. J'utilise tgθ = sin Δδ / (cos Δδ . sin (Δα. cos δ)) de Smolinsky, 2006. Il n'y a pas de commentaire sur cette formule dans sa publication et Meeus n'aborde pas le sujet. Je n'ai donc pas d'a priori sur le choix de la formule. Il y a quand même un écart de 0,065° entre nos résultats ce qui n'est pas négligeable devant les incertitudes de nos mesures.
Quant aux corrections de précession, j'utilise la méthode décrite par Meeus au chapitre 14. Les calculs sont assez fastidieux avec des coefficients intermédiaires zêta, êta, thêta, A, B et C à calculer. Mes résultats sont très différents des tiens, mais je pense que l'erreur vient de chez moi. J'aimerai bien savoir quelle méthode tu as utilisée.